Summary
The application of artificial intelligence recently has gained a great deal of attention in the oil and gas industry and appears in various studies in petroleum engineering. With the usage of machine learning and deep learning algorithms, reservoir behaviors can be predicted and interpreted from the available historical data without relying on complicated physical models. In this study, the convolutional and recurrent neural networks will be combined into the generative adversarial network (GAN) architecture to predict the oil production rate. We first use machine learning models based on XGBoost algorithms to extract the important features for further training phase of the GAN model, then we develop the deep learning model based on GAN architecture, and present the step by step workflow to train the model and predict future oil production rate.
In GAN architecture, the long short-term memory (LSTM) network will be employed as generator and the convolutional neural network (CNN) will be implemented as discriminator. A new feature will be generated from the LSTM network, then incorporated with previous training data to feed in the CNN discriminator and produce the predicted oil rate. By using the mean square error loss function to minimize the discrepancy between real and predicted values, the LSTM and CNN models then will be trained simultaneously on the training data, evaluated on the validation data, and proved the generalization capability on the test data. The results of four oil wells from field cases have demonstrated the applicability of the model to simulate and predict the behavior of oil well performance.
Model
Originally, GAN is proposed by Ian Goodfellow et al. in 2014, the model is trained to learn the statistical pattern of input data wherein the model can be used to generate the output that is similar to the input and widely applied in image generation, video prediction, and voice generation. There are two fundamental components of the generative adversarial network (GAN) which are generator network and discriminator network. In this study, we will slightly modify the GAN architecture to satisfy the regression task of predicting the oil production rate. Figure below shows the development of the GAN model in this study. The GAN model consists of two different networks: LSTM in generator and CNN in discriminator.
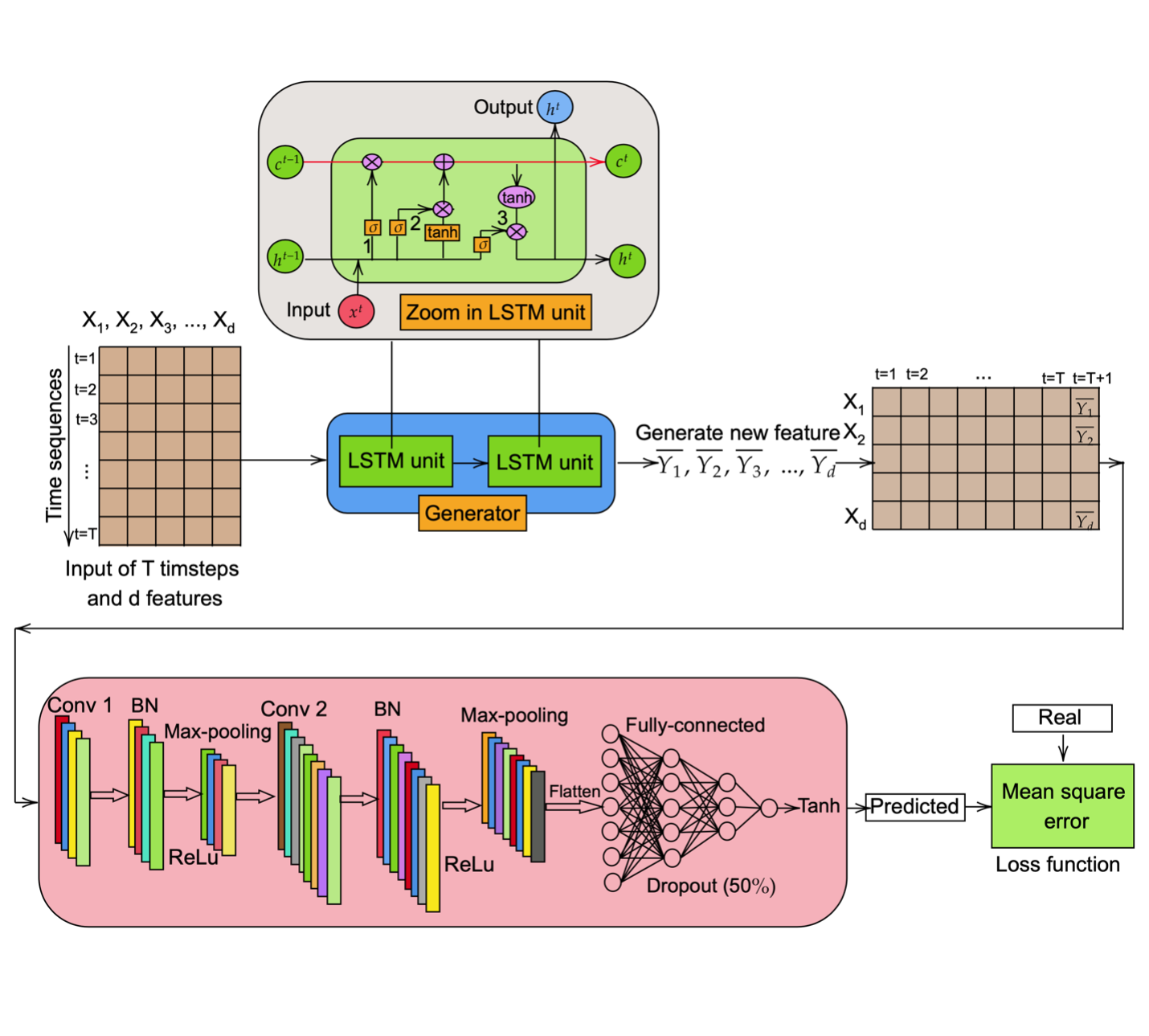
The input data is made up of $T$ timesteps and $d$ features. The format of input data is as follows:
$$ X = [X_1, X_2, X_3, \dots, X_d] $$
where each column in input $X$ is a sequence of $T$ timesteps.
$$ X_i = \begin{bmatrix} X^1_i, X^2_i, X^3_i, \dots, X^T_i \end{bmatrix}^T, \quad \forall i = \overline{1 \dots d} $$
The input $X$ is fed into the LSTM (generator) network which consists of two LSTM units inside. As depicted in figure above, when we zoom in on the LSTM unit, there are several gates wherein the input data, previous hidden and cell state will pass through. To give better a intuitive view of LSTM, firstly, we define the parameters of the LSTM network as follows:
$$ W = \begin{bmatrix} W_f \ W_i \ W_c \ W_o \end{bmatrix}, \quad U = \begin{bmatrix} U_f \ U_i \ U_c \ U_o \end{bmatrix}, \quad b = \begin{bmatrix} b_f \ b_i \ b_c \ b_o \end{bmatrix} $$
where $W$ and $U$ are weight matrices and $b$ is bias vector; and $f$, $i$, $o$, $c$ indicate the forget gate, update gate, output gate, and cell state, respectively. The ability of LSTM to memory information that passes through the network comes from the cell state which is the red horizontal line running through the LSTM unit. At time step $t$, then input $X^{t}$ and the previous hidden state $h^{t-1}$ will pass through the forget gate (denote as 2).
$$ f_t = \sigma(W_f x_t + U_f h_{t-1} + b_f) $$
The second gate is the update gate which retains the information from the previous step to the cell state. There are two layers in this process: a sigmoid layer that decides the updated values and a tanh layer that creates new values. The output from those calculations will be added together with the output from forget gate through the element-wise multiplication operation $(\otimes)$ into the cell state (denote as 2).
$$ i_t = \sigma(W_i x_t + U_i h_{t-1} + b_i) $$
$$ \tilde{c}_t = \tanh(W_c x_t + U_c h_{t-1} + b_c) $$
$$ c_t = f_t \otimes c_{t-1} + i_t \otimes \tilde{c}_t $$
Finally, the output gate (denotes as 3) will control the output values from the LSTM unit. The mathematical expression is as follows:
$$ o_t = \sigma(W_o x_t + U_o h_{t-1} + b_o) $$
$$ h_t = o_t \otimes \sigma(c_t) $$
The output from the LSTM generator is transformed to the length of the input sequence, then reshaped and concatenated with the original input sequence to obtain a new input sequence that will be fed to the CNN discriminator. In the actual design architecture, there are two fully connected layers and a tanh activation layer at the end of the LSTM network:
$$ Y = \begin{bmatrix} \bar{Y}_1, \bar{Y}_2, \bar{Y}_3, \dots, \bar{Y}_d \end{bmatrix} $$
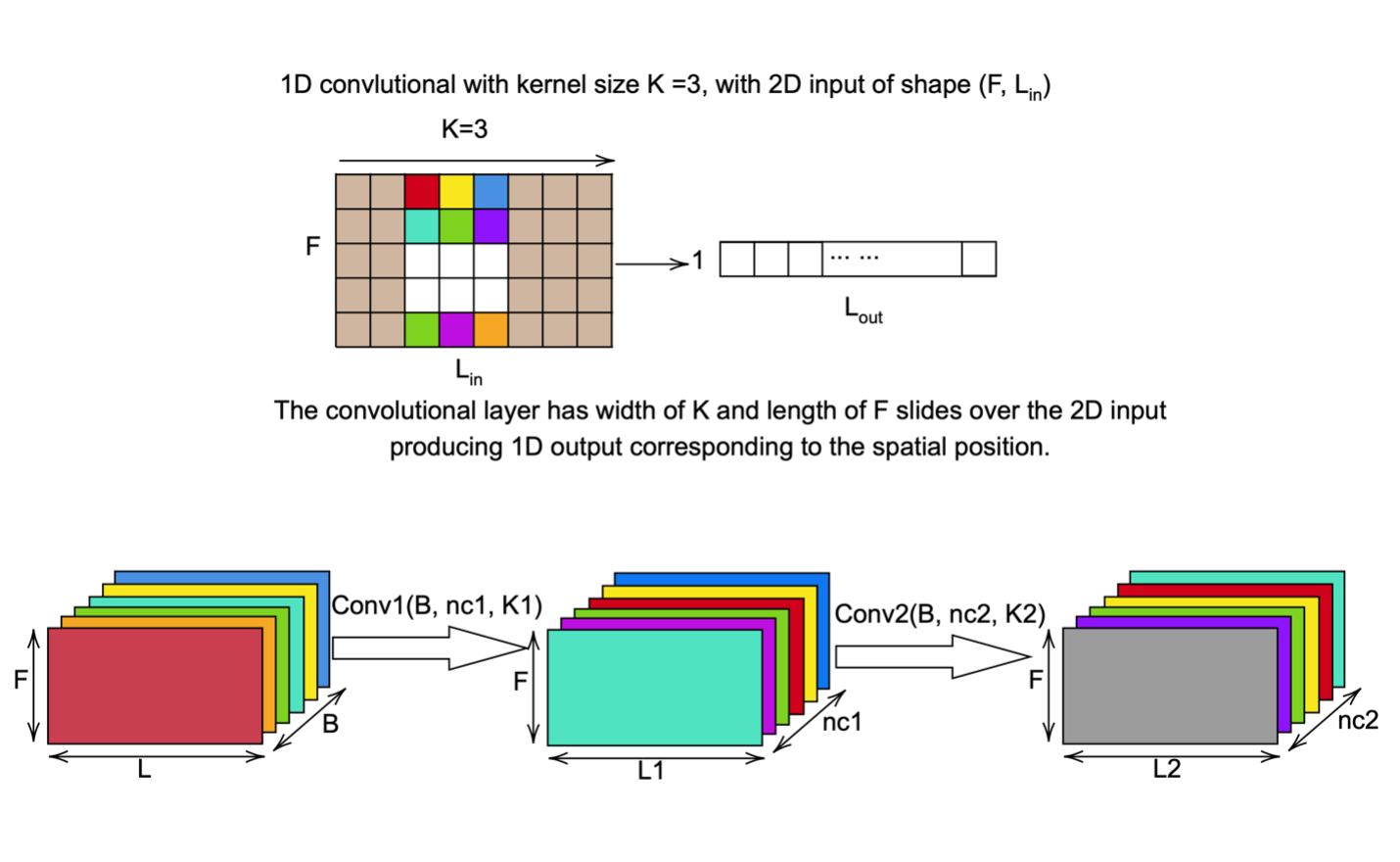
We used a different architecture of discriminator. The CNN discriminator consists of two one-dimensional (1D) convolution layers, two batch normalization (BN) layers followed by two ReLU activation layers, two max-pooling layers, and two fully connected layers at the end. The first convolutional layer (Conv 1) receives the information from the LSTM generator and input sequences, then followed by a batch normalization layer and ReLU activation layer, and connected with the second convolutional layer (Conv 2) via a max-pooling layer. In accordance with the previous design, the second convolutional layers (Conv 2) are also followed by the batch normalization, the ReLU activation, and the max-pooling layers. Next, a flatten layer will be employed to convert the data into a one-dimensional array which is the input for the next two fully connected layers. Two dropout layers with a fifty percent probability of randomly dropping the units are also added to the networks to prevent the model from overfitting problem. Finally, the output from the whole GAN model is calculated through a tanh activation function wherein the output lies on the range from -1 to 1.
The input for the CNN discriminator has the shape of $(B, F, L )$, where $B$ is the batch size, $L$ is the sequence length (lag time or look back data), and $F$ is the number of features. Noting that the sequence length of CNN is now transposed to have more than one-time step compared to input length for LSTM.
On the advantages of this design of GAN, the batch norm layer help to train the networks faster and more stable since the output from previous layers is normalized and scaled into standard distribution, while the ReLU non-linear activation function help to deal with the vanishing gradient problem and less computational expensive than other activations such as tanh or sigmoid. As previously mentioned, dropout help to prevent the overfitting problem, and the max-pooling layers help to reduce the number of parameters, hence, improve the performance and avoid the overlearning problem.
It is worth noting that the loss function used in this study was mean square error which is different from the original proposed GAN model in literature since the task we tackled was a regression problem. By minimizing the discrepancy between the actual and predicted values through the loss function, the GAN model can learn from the historical data to capture the trend and be able to predict future performance. Finally, both generator and discriminator are trained simultaneously and iteratively.
Finally, the objective function is:
$$ \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} \left( \hat{y}_i - y_i \right)^2 $$