Coupling neural networks and particle swarm optimization
1. Introduction
History matching is one of the most important tasks in reservoir engineering and is defined as the process of finding an appropriate set of parameters which best represents dynamical behavior of an oil and gas system. History matching is often an ill-posed problem, which means there is no unique solution to the problem. Due to the complexity and computational expense of reservoir simulation runs, there is an alternative approach of coupling a neural networks and particle swarm optimization to solve the history matching problem.
Here, we are about to design a machine learning model (specifically a neural net) to perform the history matching of an black oil reservoir. The oil field has been producing for 50 years. Historical data contains all of the information of dynamical simulation and production. There are a total of 187 simulation runs with certain output, and 15 reservoir properties within the corresponding ranges.
2. Overview of a neural network
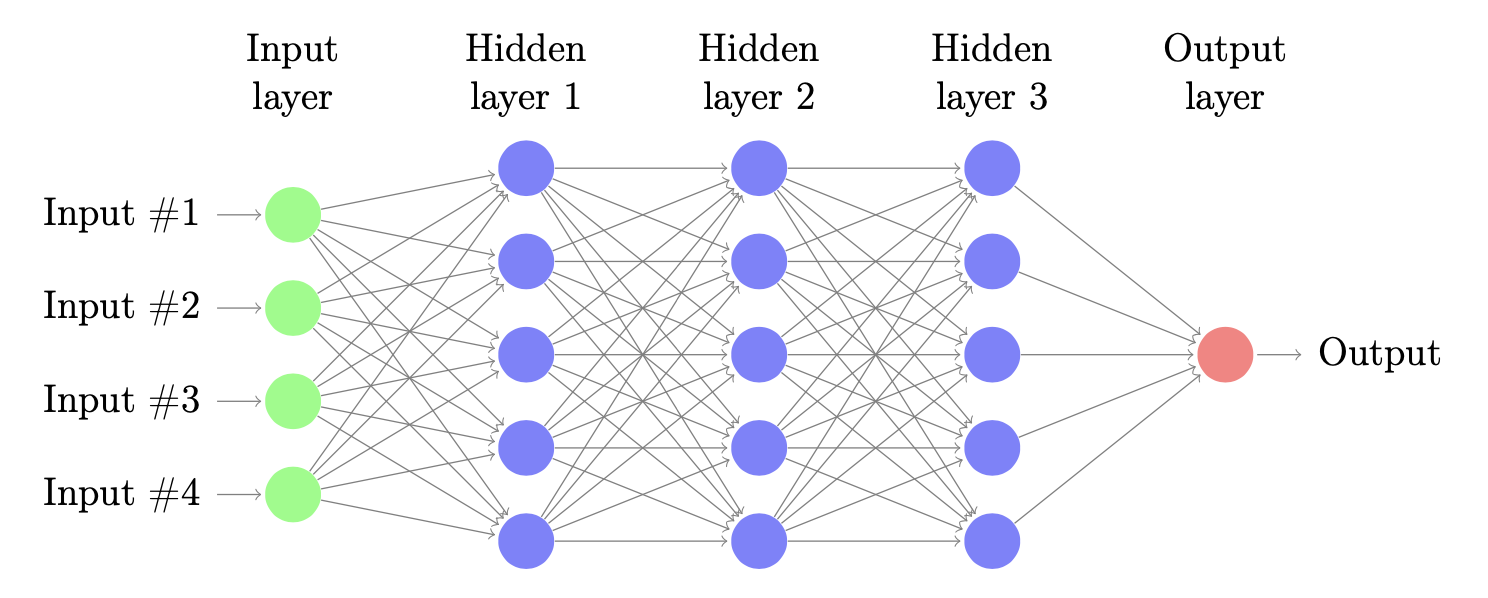 In a typical multi-layer neural networks, beside the input and output layers, there are several hidden layers in the middle. Figure above is an example of fully connect multi-layer neural network with three hidden layers. Let denote the output of each unit as $a$, therefore the output of a layer $(l)$ is $\mathbf{a}^{(l)}$. In a neural network of $L$ layers, there are corresponding $L$ matrices of coefficients ($\mathbf{W}^{(l)} \in \mathbb{R}^{d^{(l)}\times d^{(l+1)}}$) that represent connection between layer $l-1$ and layer $l$. Note that layer $0$ is the input layers. Bias of layer $l$ is usually denoted by $\mathbf{b}^{(l)} \in \mathbb{R}^{d^{(l)}}$. We then can define $\mathbf{\theta}^{(l)} = [\mathbf{b}^{(l)}, \mathbf{W}^{(l)}]$ as the weight matrix of layer $(l)$. The output from each layer can be written as:
In a typical multi-layer neural networks, beside the input and output layers, there are several hidden layers in the middle. Figure above is an example of fully connect multi-layer neural network with three hidden layers. Let denote the output of each unit as $a$, therefore the output of a layer $(l)$ is $\mathbf{a}^{(l)}$. In a neural network of $L$ layers, there are corresponding $L$ matrices of coefficients ($\mathbf{W}^{(l)} \in \mathbb{R}^{d^{(l)}\times d^{(l+1)}}$) that represent connection between layer $l-1$ and layer $l$. Note that layer $0$ is the input layers. Bias of layer $l$ is usually denoted by $\mathbf{b}^{(l)} \in \mathbb{R}^{d^{(l)}}$. We then can define $\mathbf{\theta}^{(l)} = [\mathbf{b}^{(l)}, \mathbf{W}^{(l)}]$ as the weight matrix of layer $(l)$. The output from each layer can be written as:
$$ \mathbf{a}^{(l)} = f(\mathbf{W}^{(l)}\mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}) = f(\mathbf{\theta}^{(l)}\mathbf{a}_{\ast}^{(l-1)}) $$
where $\mathbf{a}_{\ast}^{(l-1)}$ is the concatenate form of a column vector of $1$ and $\mathbf{a}^{(l-1)}$.
Now, we can define the loss function between the output or model response and actual data or observations. In a regression probelem, mean square error (MSE) function is often used because it is a convex function as well as for easier calculation of derivatives. That means we can apply gradient-based optimization techniques. The loss function is defined as:
$$ J(\mathbf{W}, \mathbf{b}) = \frac{1}{N}\sum_{i=1}^{N}||{y_i - \hat{y}_i}||_2^{2} $$
where $\mathbf{W}, \mathbf{b}$ are two sets of all weight matrices $\mathbf{W}^{l}$ and biases $\mathbf{b}^{l}$, $y_i$ is model output from neural network and $\hat{y}_i$ is actual data. Or:
$$ J(\mathbf{\theta}) = \frac{1}{N}\sum_{i=1}^{N}||{y_i - \hat{y}_i}||_2^{2} $$
In training neural network or machine learning model, gradient descent (GD) and its variants are by far the most popular techniques. Gradient descent is an algorithm used to optimize the objective function $J(\mathbf{\theta})$, with respect to the parameter $\mathbf{\theta} \in \mathbb{R}^d$, by gradually updating the parameter $\mathbf{\theta}$ in the opposite direction to the gradient of the objective function. The learning rate $\eta$ determines the size of each backward jump of $\mathbf{\theta}$. The advantages of GD are the ease of implementation and low memory cost, while the drawback is the convergence time or local minima. In machine learning or deep learning area, we use this algorithm to update model weights $\mathbf{\theta}$. The general definition of gradient descent is followed by:
$$ \mathbf{\theta} = \mathbf{\theta} - \eta\nabla J(\mathbf{\theta}) $$
3. Particle Swarm Optimization (PSO)
The idea behind PSO algorithm is particles will communicate the information they find with others, and update their velocity based on the local best (pbest) and global best particle (gbest). The swarm will update best result as when the new global best is found, and each particle tend to move toward the personal best and global best.
Particle Swarm Optimization (PSO) is a population based stochastic optimization technique that inspired by social behavior of bird flocking or fish schooling. PSO is the global optimizer which aims to find global minima or maxima of an objective function. The general update rule for PSO algorithm is followed:
PSO:
Evaluate the fitness
Calculate the velocity
$$ v_i^{t+1} = wv_i^{t} + c_1r_1(pbest^{t} - x_i^{t}) +c_2r_2(gbest^{t} - x_i^{t}) $$
Update the particle position (or solution)
$$ x_i^{t+1} = x_i^{t} + v_i^{t+1} $$
The hyper-parameters used in PSO are: - $w$ is an inertial weight usually slightly less than 1 - $c_1$ is the cognitive weight, represents the impact of personal best on individual particle’s movement - $c_2$ is the social weight, represents the impact of global best on individual particle’s movement - $r_1$, $r_{2}$ are two random components, represent the randomness of the process of updating particle’s velocity. These two also represent the stochastic search of direction.
4. Results
You can see this GitHub repository for some results as well as detailed implementation.