Groundwater modeling and solute transport in an unconfined aquifer
We develop a control volume finite element method (CVFEM) to simulate groundwater flow, solute transport, and groundwater age in an aquifer under prograding delta or evolving grid domain. We then hypothesize that onshore saline groundwater within unconfined aquifer in delta system may have resulted from rapid propagation of shoreline during Holocence which was around 12k years ago. Numerical solutions to groundwater age equation are obtained using triangle elements with evolving grids of the domain. Sensitivity analyses are performed using a range of model settings to extract the key parameters that control the groundwater age, and salinity concentration. Results show that groundwater ages are largely affected by two confining units in Bengal delta. These age distributions are young in recharge areas , and old near the shore lines.
Summary
The fundamental equation that governs the groundwater flow in an aquifer for incompressible fluid is described as follows:
$$ \frac{\partial}{\partial x} \left( K_{xx} \frac{\partial h}{\partial x} \right) + \frac{\partial}{\partial z} \left( K_{zz} \frac{\partial h}{\partial z} \right) + C (\rho_{\text{rel}} - 1) = S_s \frac{\partial h}{\partial t} $$
where $K_{xx}$ and $K_{zz}$ are hydraulic conductivity $(LT^{-1})$ in $x$ and $z$ dimensions, $h$ is hydraulic head ($L$), $S_s$ is specific storage ($L^{-1}$), $C$ is concentration of saltwater. The hydraulic head is estimated as:
$$ h = \frac{p}{\rho_w g} + z $$
The governing equation is for age transport with uniform porosity is:
$$ \frac{\partial \tau}{\partial t} = \nabla \cdot \left(\mathbf{D} \cdot \nabla \tau\right) - \nabla \cdot (\mathbf{v} \tau) + 1 $$
In two dimensions, the equation becomes:
$$ \frac{\partial \tau}{\partial t} = \frac{\partial}{\partial x} \left[ D_{xx} \frac{\partial \tau}{\partial x} + D_{xz} \frac{\partial \tau}{\partial z} \right] + \frac{\partial}{\partial z} \left[ D_{zz} \frac{\partial \tau}{\partial z} + D_{zx} \frac{\partial \tau}{\partial x} \right] - \frac{\partial}{\partial x} \left[ K_{xx} \frac{\partial h}{\partial x} \right] - \frac{\partial}{\partial z} \left[ K_{zz} \frac{\partial h}{\partial z} + C (\rho_{\text{rel}} - 1) \right] + 1 $$
where the dispersion tensor $\mathbf{D}$ is defined as:
$$ D_{xx} = \alpha_L \frac{v_x^2}{|v|} + \alpha_T \frac{v_z^2}{|v|} + D $$
$$ D_{xx} = \alpha_L \frac{v_z^2}{|v|} + \alpha_T \frac{v_x^2}{|v|} + D $$
$$ D_{xx} = (\alpha_L - \alpha_T) \frac{v_x v_z}{|v|} $$
and $\alpha_L(L)$ is longitudinal dispersivity, $\alpha_T(L)$ is transverse dispersivity, $v_x$ is groundwater velocity in $x$ direction, $v_z$ is groundwater velocity in $z$ direction, $D$ ($L^{2}T^{-1}$) is molecular diffusion of saltwater, and $\tau(T)$ is groundwater age.
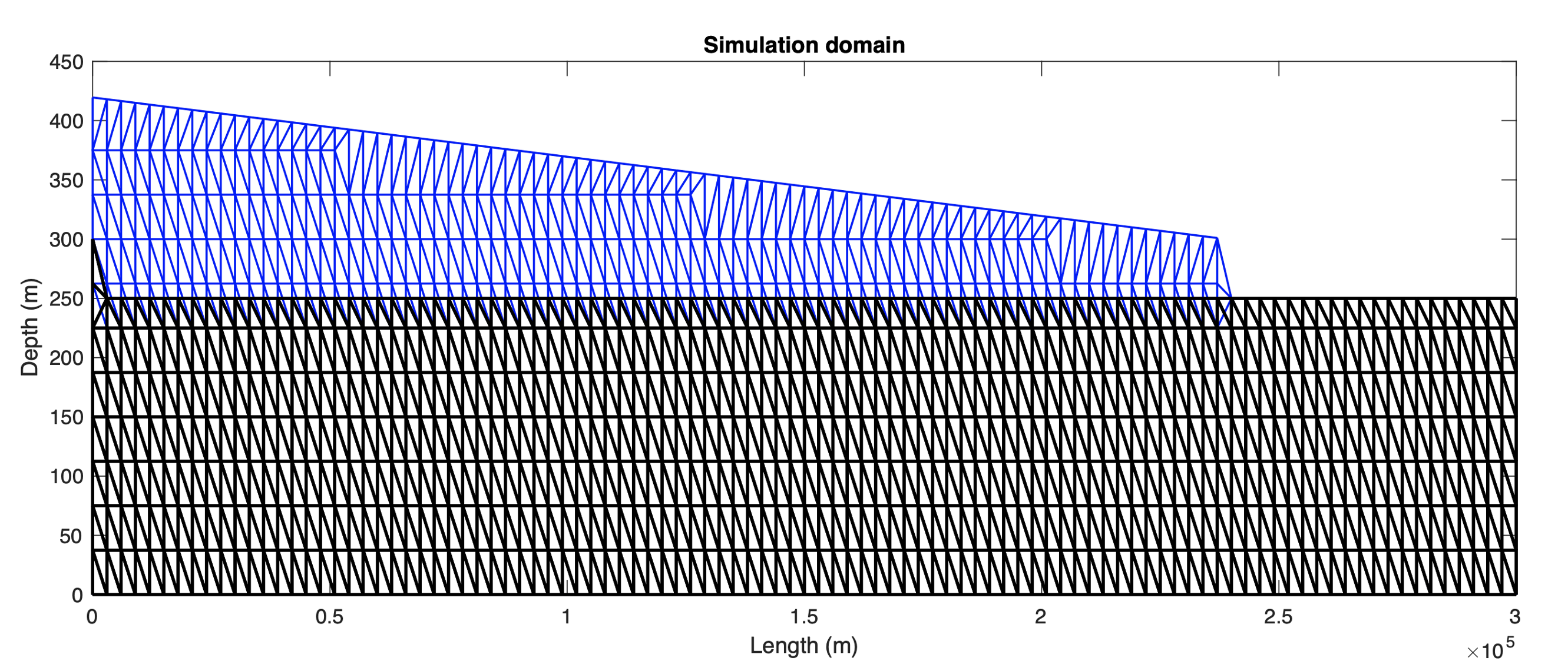
To simplify the domain as much as possible, we only depict the Bengal delta with a very coarse and simple conceptual 2D domain (figure above). The simulation domain of this model is in two dimensions (length and depth), and the top domain evolves over time. The model is represented by triangular mesh using a built-in function in MATLAB. We employed a straightforward mesh technique by joining x and z coordinates, then use a Delaunay triangulation from the points in a matrix P that contain x and z coordinates. The recharged area is located at the uppermost portion of the domain and discharged area is located at basement, which is at the same level as the sea level. We imposed no-flow boundaries for left, right, and bottom edges of the domain. Above sea level, we set salinity concentration to be zero.
Results
Here are final results from running simulation for ~ 16000 years.
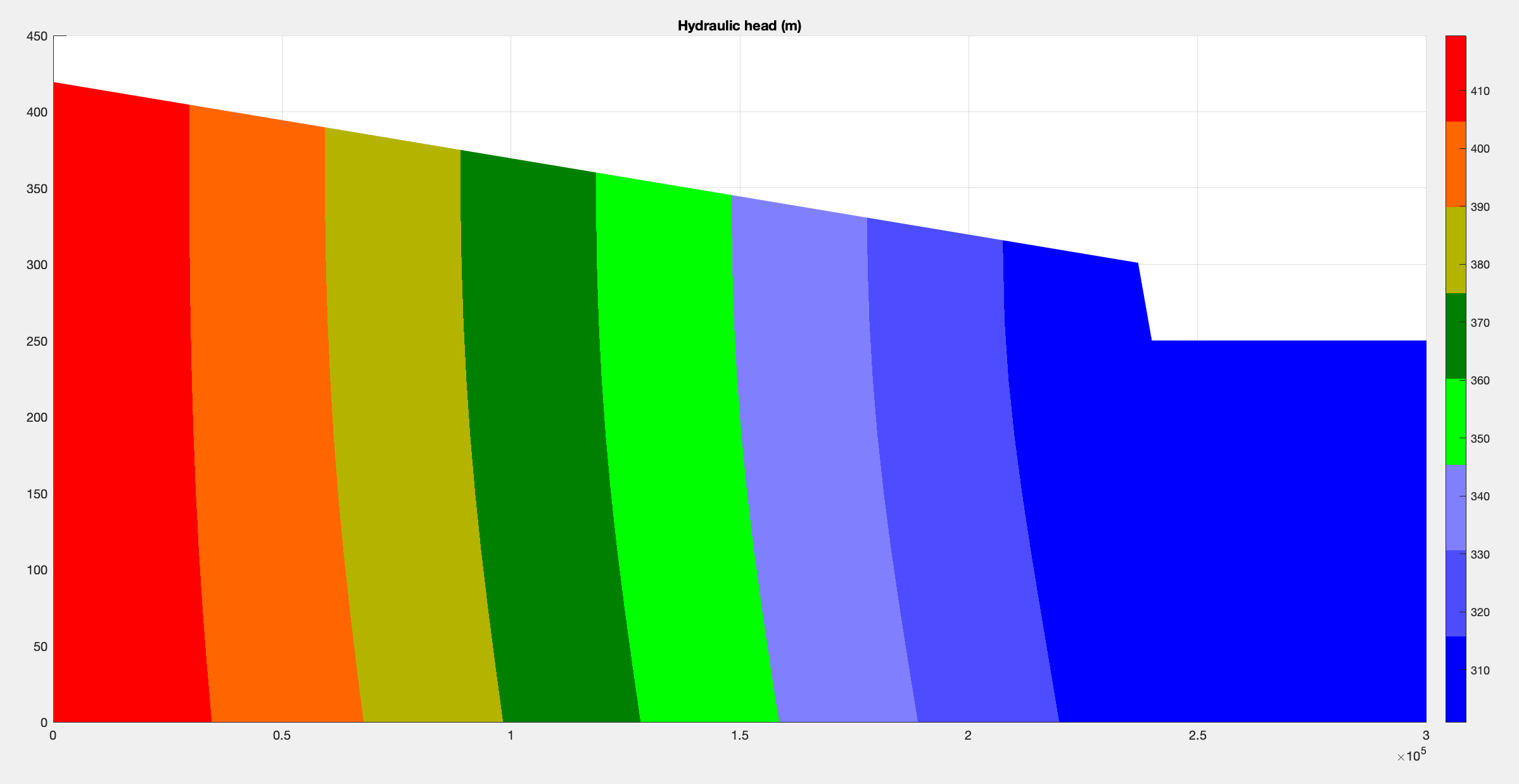
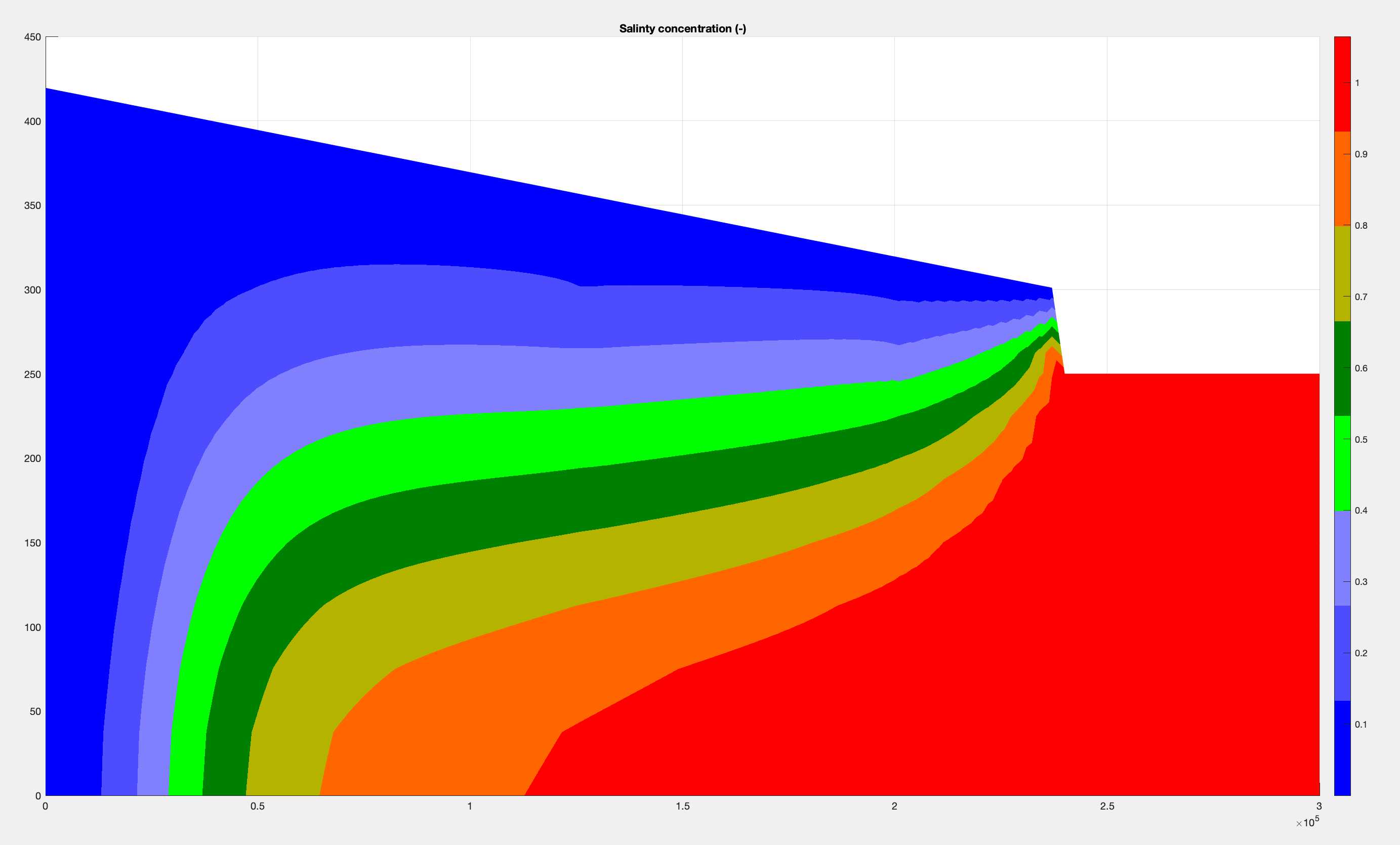
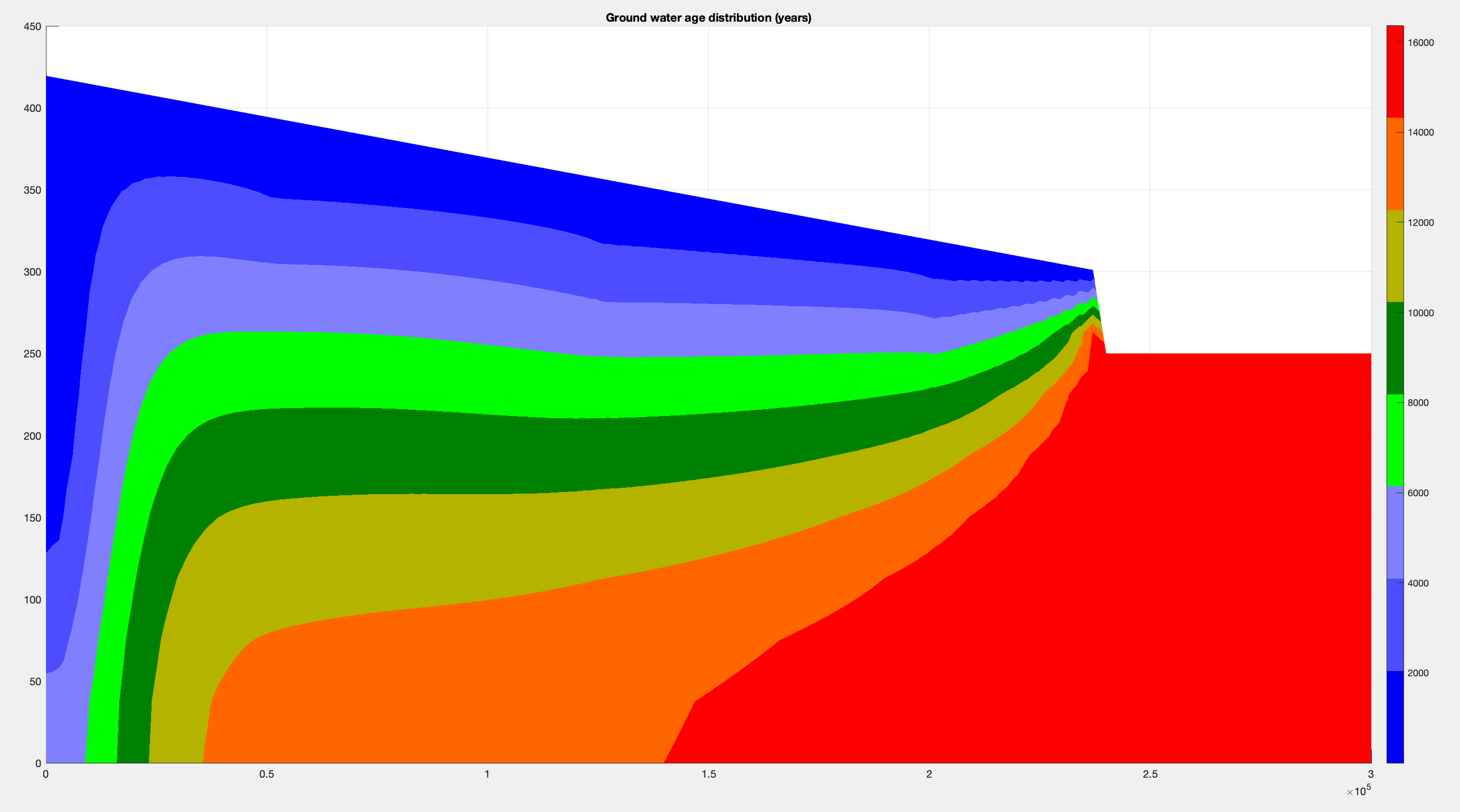
Below is a gif showing concentration evolves over time:

You can see this GitHub repo for some results as well as detailed implementation.